Un peu de théorie instrumentale…

Les plus réfractaires aux mathématiques peuvent passer cette section sans souci — cela ne vous empêchera en rien de construire et d'utiliser Sol'Ex ! Pour les autres, voici une brève justification des choix de conception de cet instrument, de sa configuration et de ses performances.

Bien que Sol’Ex soit un spectrohéliographe, il fonctionne avant tout comme un spectrographe, un instrument qui décompose la lumière en ses longueurs d’onde, ou en ses "couleurs", pour ainsi dire. Pour Sol’Ex, j’ai opté pour une configuration optique classique mais éprouvée — un choix sûr !

Le schéma optique de Sol'Ex est illustré dans la figure suivante :

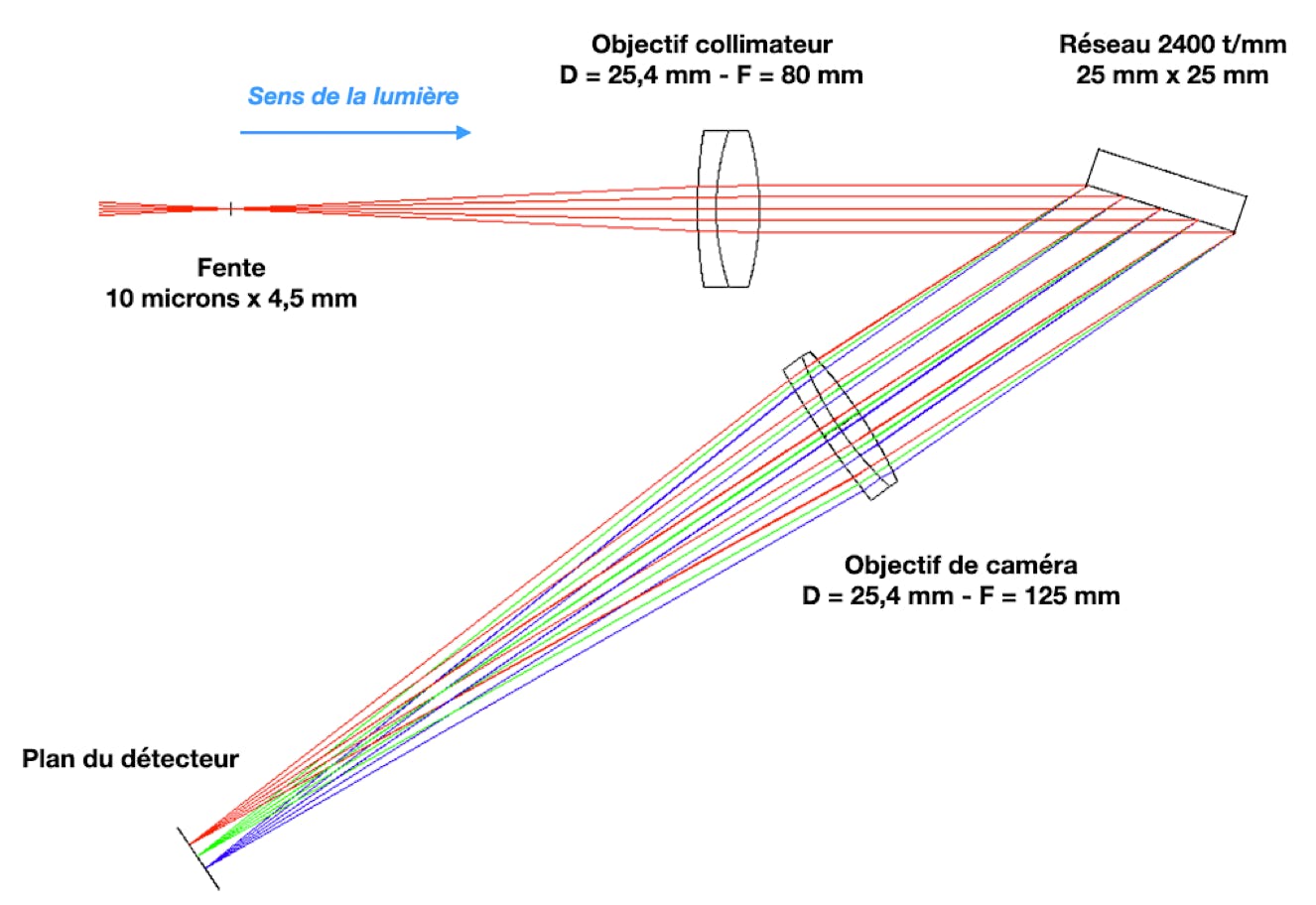
L’instrument comprend à l’origine une fente d’entrée étroite de 10 microns de large et 4,5 mm de haut, placée au foyer de la lunette d’observation. Ensuite, un objectif collimateur de 80 mm de focale, constitué de deux lentilles collées, rend les rayons lumineux parallèles après leur passage par la fente. Ces rayons rencontrent alors un réseau de diffraction holographique de 2400 traits/mm, chargé de disperser la lumière selon ses longueurs d’onde. Enfin, un objectif de 125 mm de focale focalise l’ensemble des rayons sur le plan du détecteur (c’est l’objectif de caméra).

Avant et après le réseau, les rayons forment un angle en « V » de 34°, appelé « angle total », qui donne à Sol’Ex sa forme distinctive.

On remarque que les rayons provenant du collimateur frappent le réseau avec un fort angle d’incidence d’environ 72° lorsqu’on observe la raie de l’hydrogène H-alpha (656 nm de longueur d’onde). Ce fort angle d’incidence entraîne un vignettage des rayons collectés par la lunette, en raison de la taille limitée du réseau (une conception pour minimiser l’encombrement et les coûts, tout en disposant d’une haute-performance, on le verra). Dans le plan de dispersion (illustré sur la figure), l’ouverture acceptée est d’environ f/10,6 ; perpendiculairement à ce plan, en tenant compte du champ couvert par la fente, l’ouverture est d’environ f/5,6.

Pour mieux comprendre, imaginons une lunette de 65 mm de diamètre et de 420 mm de focale. Son rapport d’ouverture est donc de 420 / 65 ≈ 6,5. En théorie, lorsque cette lunette est utilisée avec Sol’Ex, son ouverture effective devient f/6,5 dans l’axe perpendiculaire au plan d’incidence (limitée par l’ouverture de la lunette) et f/10,5 dans le plan d’incidence (limitée par Sol’Ex). Si l’on pouvait dessiner la surface utile d’entrée, elle aurait la forme d’une ellipse, et non d’un cercle.

Ce dimensionnement occasionne une perte de flux, car l’objectif de la lunette est diaphragmé (sauf si l’on utilise une lunette à ouverture native proche de f/10). Toutefois, cette perte est négligeable en observation solaire grâce à l’abondance de lumière. Les lunettes et objectifs photographiques ayant des ouvertures entre f/5,6 et f/9 fonctionnent avec Sol’Ex sans effet notable sur la finesse des images. Pour les instruments très ouverts, vous pouvez essayer différents diaphragmes à l’entrée de votre lunette afin de réduire son ouverture et d’observer d’éventuelles améliorations. Des exemples sont fournis dans la section « Observation ». Par exemple, pour un objectif photographique à f/2,8, il est conseillé de le diaphragmer à f/6 ou même f/7 (la diffraction reste sans impact significatif sur les performances de Sol’Ex dans ce cas).

En même temps que le fort angle d’incidence sur le réseau réduit légèrement le flux lumineux, il améliore la finesse du spectre enregistré. Pour comprendre ce phénomène, il faut noter la différence de taille du faisceau lumineux dans le plan d’incidence avant et après le réseau (respectivement D1 et D2) :

Cette caractéristique propre à l’utilisation d’un réseau est appelée anamorphose. En plus d’influencer la taille des faisceaux lumineux avant et après le réseau, l’anamorphose modifie aussi la taille de l’image de la fente sur le détecteur. La largeur de cette image est réduite d’un facteur D1/D2, nommé le facteur d’anamorphose, tandis que la taille dans l’axe spatial (perpendiculaire à l’axe de dispersion) reste inchangée. Pour illustrer cet effet, l’image suivante montre une fibre optique qui remplace temporairement la fente de Sol’Ex : initialement circulaire, l’image finale de la fibre apparaît ovalisée.

Aspect que quelques images monochromatiques d’une fibre optique disposée à l’entrée de Sol’Ex pour les longueurs d’onde voisine de la raie H-alpha.

L’anamorphose, en réduisant optiquement la largeur de la fente, a un impact notable sur le pouvoir de résolution spectral de Sol’Ex, permettant de révéler plus de détails dans le spectre. Cet effet est particulièrement bénéfique pour Sol’Ex, contribuant à ses hautes performances malgré son format compact.

Calculs pratiques

Commençons avec une formule reliant l’angle total G (dans Sol’Ex, G = 34°) et l’angle d’incidence α sur le réseau :

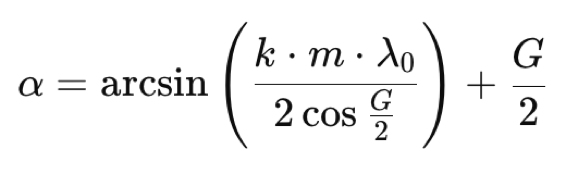
Avec k, l’ordre de diffraction (ici k = 1), m, la densité de gravure (ici m = 2400 traits/mm) et λ0, la longueur d’onde au centre du capteur (ici 0,6563x10^-3 mm). Par ailleurs G = α - β, avec β, l’angle de diffraction.

Pour l’observation de la raie H-alpha (6563 A) et en adoptant l’angle total de 34°, l’angle d’incidence des rayons sur le réseau est précisément α = 72,4° alors que l’angle de diffraction (après le réseau) est β = 38,4°. La facteur d’anamorphose est donné par la formule :

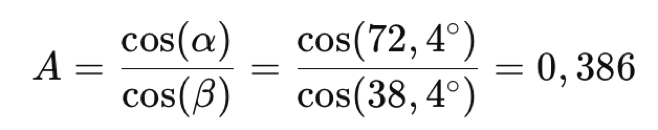
Ce facteur signifie que la largeur de la fente d’entrée est réduite en quelque sorte. (optiquement ) à 0,386 x 10 microns = 3,86 microns. C’est ce résultat qui provoque un gain en résolution spectrale. Il faut ajouter que vers la raie rouge de l’hydrogène, mais aussi une large partie du spectre visible, l’optique de Sol’Ex est quasi limitée par la diffraction, c’est-à-dire qu’elle est très bonne (dès lors que l’on n’explore par simultanément un domaine spectral très large).

Voyons à présent le calcul du pouvoir de résolution.

Le pouvoir de résolution R est défini par la formule R = λ / Δλ, avec λ la longueur d’onde d’observation et Δλ le plus fin détail observé dans le spectre en unité de longueur d’onde. On remarque que R est un nombre sans dimension. Plus est R est grand, plus on observe de petits détails dans le spectre. Nous avons :

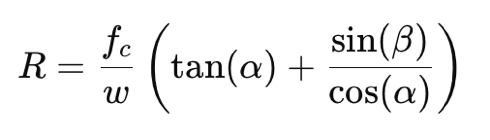
avec on l’a vu, α et β, respectivement les angle d’incidence et de diffraction sur le réseau. Par ailleurs, fc est la distance focale du collimateur, ici fc = 80 mm, et w est la largeur physique de la fente, ici w = 10 microns = 0,010 mm. Le phénomène d’anamorphose est décrit par le terme entre parenthèse de cette formule, ainsi que l’impact de la densité de gravure du réseau. Calculons autour de la raie H-alpha :

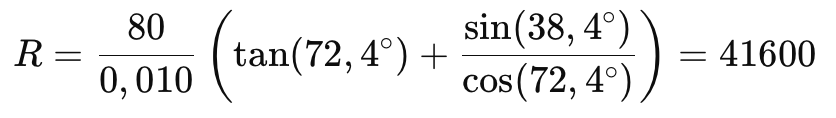
En tenant compte des aberrations optiques, on peut considérer que le pouvoir de résolution de Sol’Ex proche de R=40000, une performance notable pour un instrument compact. Cela donne une finesse spectre de Δλ = λ / R = 6563 / 40000 = 0,16 A = 0,016 nm,  plus étroite que celle de filtres interférentiels bien plus coûteux.

Dispersion spectrale et échantillonnage

Le paramètre de dispersion spectrale, désigné par r, et que l’on exprime ici en A / pixel est donné par :

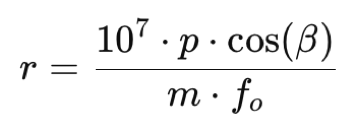
avec p, la taille des pixels en millimètres et fo, la longueur focale de l’objectif de caméra, soit ici fo = 125 mm. Avec un capteur type Sony IMX178, par exemple, la taille du pixel est de 2,4 microns,

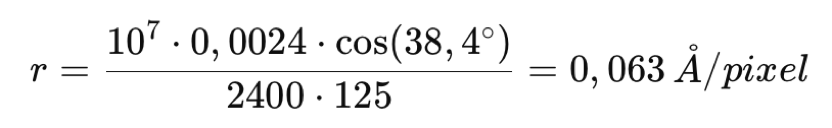
Il est important de mettre en regard l’élément de résolution spectral Δλ calculé précédemment, soit 0,16 A et l’échantillonnage du spectre par les pixels du détecteur, 0,063 A/pixel. Il apparaît que l’on a 0,16 / 0,063 = 2,53 pixels par élément de résolution, c’est-à-dire que l’on se situe au-dessus de la limite de Shannon (ou Nyquist) qui est de deux points d’échantillon par élément de résolution. C’est un bon dimensionnement pour Sol’Ex. Noter que si le capteur IMX178 est exploitée en binning 2x2 (équivalent de pixels de 4,8 microns) on ne respecte pas le critère de Shannon, et donc de l’information est perdue. Pour les travaux qui demandent une grande précision (des mesures Doppler en particulier), il est préférable d’utiliser une caméra à petits pixels et travailler en binning 1x1, dans la mesure du possible.